Echography simulation

Here we'll see how the Lattice-Spring Model (see Computational simulations of dynamical systems) can be used to simulate the dynamics of mechanical waves in bodies that can be deformed under external perturbations. More specifically, we will see how to infer some of the properties or internal structure of a body by looking at its surface's response to mechanical perturbations, like an echography.

Echography (or sonography) is an imaging technique that uses mechanical waves to induce vibrations in a medium and produce images of its structure based on the reflections of waves. In medicine, medical ultrasound uses ultrasound waves to produce images of internal body structures such as organs, joints, muscles, etc. Ultrasound machines use piezoelectric transducers to generate and detect mechanical vibrations on a surface; the perturbations generated in the surface propagate as longitudinal pressure waves inside the medium and are reflected by the internal structures of the body to return to the surface and be detected by the transducer. An image is then formed by looking at the time delays and intensities of the reflected waves.

THE PROBLEM Let's consider a segment of a body with a plane surface divided in cells. We want to perturb this entire surface and then observe how each cell on the surface moves or vibrates in time. Each cell will have a different response depending on the waves that are reflected by the structure that is under it. From this, we want to infer the internal structure (e.g. mass density, elasticity) of the segment of the body that is right under each cell. Once we have a map of the structure under each cell, we'll have a complete map of the internal structure under the surface we are considering.

SIMULATION (LSM)

For the computational simulation of the body we consider again a simple cubic lattice formed by masses joined to their 6 nearest neighbors by springs and dampers.

We will simulate the body with a chosen mass density distribution, then we will try to reconstruct its distribution by purely looking at the surface's vibrations. The evolution in time of such system is described by the LSM equation:

Here N stands for the number of neighbors attached to the mass with index i (N=6 for every mass in this case). We could simulate the initial perturbation by letting all the masses in the lattice to begin at rest but giving an initial force or velocity to the masses on the top surface and then let the waves propagate throughout the body. We'll make the masses on the bottom surface to stay fixed, as if there were a very dense barrier under the body that will completely reflect the waves coming from the top surface; this will avoid the center of mass of the body to gain a velocity after the initial pulse and move throughout the simulation without anything stopping it. For simplicity we will consider all the springs to have the same stiffness and all the dampers to have the same damping coefficient, however, the body will have a non-uniform mass density distribution, so obviously the masses in the lattice won't be all the same.

Once we have the LSM equation and the initial conditions we use the Verlet algorithm to integrate the equations of motion.

THEORETICAL MODEL

We can start by considering one-dimensional longitudinal pressure waves. Notice that in this simplification we assume that the vibrations in a longitudinal segment of the body aren't affected in a significant way by the vibrations of the neighboring parallel segments. As we'll see, this approximation is good enough for our computational system, even when the masses are joined to their lateral neighbors. We can then consider parallel chains of masses that go from the top surface to the bottom, each mass joined to its two neighbors by a spring and a damper. Using the LSM equation with

we get, in terms of the displacement from the equilibrium position

were we have used

We can write

Reordering the terms and multiplying by the equilibrium separation between masses

And if we let

we get the first spatial derivatives

and then

with

These are the mass density, the elastic or Young's modulus and a diffusion coefficient. In the process of letting the number of masses go to infinity and equilibrium spacing go to zero, the masses also go to zero, and the stiffness constant and the damping coefficient go to infinity, so we have to express these in terms of the finite parameters shown above. We now have an analytical equation for longitudinal waves propagating in a system like the one we proposed using the Lattice-Spring model.

For covenience we can write

with

The first coefficient will turn out to be the velocity of propagation. The second coefficient corresponds to a diffusive term; when this coefficient is zero, we get the wave equation.

We'll use separation of variables, proposing a solution of the form

Substituting it into the PDE we get

Where lambda is a constant. According to our model, masses in the top surface must be free to vibrate, while masses on the bottom surface are fixed. So as boundary conditions we have

so, for the spatial part we get solutions of the form

The temporal part then takes the form

If we propose exponential solutions

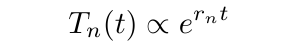
We get

When the discriminant is negative:

oscillatory solutions are obtained. This happens when

We'll therefore divide the solutions in two sets; the oscillatory solutions and the non-oscillatory solutions

Notice the if the elastic modulus and the density (or the impedance) of the body is high compared to the diffusion coefficient, then the non-oscillatory solutions are negligible, as this solutions will be associated with large values of n, and the solutions decrease exponentially with lambda, which is proportional to n squared. This means that if the body is rigid enough its mechanical response is purely vibrational. So if we use reasonable parameters then we can consider the oscillatory solutions only.

We then end up with complex temporal solutions of the form

where we have used

So we can write the complete solutions as

The initial conditions of the body beginning at rest and the top surface having an initial velocity we will express using Dirac's delta as

From the first condition we get

and from the second condition

We use the orthogonality of the cosine functions to get

where

then

So the complete solutions are

As in the analytic model we're using an idealized initial condition assuming that the infinitesimal segment of mass that is in the surface has an infinite initial velocity and in the simulation we have finite masses that can only take finite velocities, we have to fix the initial velocity in the simulation that matches the theoretical assumption.

The comparison between the surface's velocity obtained with the analytical model and the simulation for a uniform mass density distribution is shown below

After the initial pulse is generated, it goes all the way from the top to the bottom surface where it is inverted and reflected to the top surface and generates a peak in the signal shown above and gets reflected again, repeating the process and producing a peak on the signal each time it reaches the top surface. As there is diffusion in the body, the pulse looses amplitude as time goes on. It can be seen that there's some disagreement between the curves that increases with time, but as the signals after the first peak are just inverted copies, we'll only care about the range in time that is before this first peak.

Notice that the time at which the first peak appears is the time it takes the pulse to travel a total distance of 2L. We get a null signal everywhere else, as the density throughout the body is uniform so there's no other barriers that can reflect the pulse but the bottom surface of the body.

Let's now analyze the oscillatory part of the solutions

At an arbitrary time, the function oscillates around zero as n increases and as the complete solutions are sums over n, the total signal is zero.

We can conveniently rewrite the delta coefficient as

If the body is rigid enough

when

for small values of n we get

and for large values of n the solutions oscillate as before.

Substituting in the oscillatory solutions we get

At this particular time the first terms of the solution doesn't oscillate around zero and therefore the signal is not null. So the peak in the signal coming from the bottom surface corresponds to this time, and therefore v must be the velocity of propagation of the wave.

The signal at this time has magnitude

This corresponds to a complete reflection, where the incident wave gets inverted after reaching an "infinite" barrier with coefficient of reflection equal to -1.

In general if the body has a non-uniform mass density then a portion of the pulse will be reflected at each density barrier. The coefficient of reflection for a given barrier is

it is a function of the impedance

So a peak in the signal at time t produced by an inner barrier with coefficient R has the size

Therefore using this equation we can determine the size of a density barrier inside the body by looking at the size of the peak it produces in the signal.

To determine the profundity from which a given signal is coming we consider the velocity of the pulse as a function of the local density

As in the analytical solution that we are using we consider an uniform density, we'll approximate the density distribution of the body to be uniform by segments by dividing the profundity of the body in N cells. As a consequence, the velocity will also be uniform by segments. So we define the velocity and density of each cell as

A pulse that is reflected right at the surface (the first cell) would by definition appear in the signal at a time

If a pulse is reflected from the second cell (right under the surface) it would take it a time

to return to the surface after it is generated.

If the wave is reflected from the third cell it would take it a time

In general

This means that in order to determine the complete density distribution of the body it is only needed to know the surface's density. Having this, we know what the pulse's velocity is until it hits a density barrier, we then calculate the size of the barrier by looking at the size of the peak produced in the signal and from this we can deduce the change in the velocity of the pulse, so by looking at the time difference between the first peak and the next one, we'll know the distance between their two corresponding density barriers. We then calculate the size of the second barrier by looking at the size of the second peak, and the process is repeated until the complete density distribution is determined in terms of the density barriers. The "resolution" of the density map will depend on the number of cells in which the body is divided. For the computational simulation, the number of cells can be as high as the number of masses in the lattice.

As a test we set up a simulation for a lattice with a chosen density distribution. We'll use a distribution of the form

which is the structure of a torus

The parameters used in the simulation were

For a lattice with size

Below we show the signal obtained for one of the surface's cells. Before the peak reflected from the bottom surface, there's two main peaks corresponding to the pulse going thru the torus structure. When the primary pulse gets partially reflected to the surface, secondary pulses arise each time the reflected pulse crosses a density barrier, then this secondary pulses repeat the process and so on. This appears as noise in the signal. Also lateral neighbors in the lattice will affect each other.

Once the signal for every cell on the surface is obtained, the complete density can be calculated for the N cells (a 40x40x40 density matrix in this case). A perpendicular cross section of the matrix will have a 40x40 cells of resolution. A cross section of the matrix obtained is shown below. Interpolation was used.

Successive cross sections of the density matrix are shown below.

References:

See partial differential equations on:

-E. Butkov (1973). "Mathematical Physics"

-G. Arfken (2005). "Mathematical methods for physicists"

-Mathew Schwartz's lecture notes on impedance http://users.physics.harvard.edu/~schwartz/15cFiles/Lecture9-Impedance.pdf -David Morin's notes on normal modes: http://www.people.fas.harvard.edu/~djmorin/waves/normalmodes.pdf